Detailed Answers of CDS-1 2021 Maths
This post contains CDS – 1 2021 maths paper solution.
[pdfviewer width=”600px” height=”849px” beta=”true/false”]https://vinnybhardwaj.com/wp-content/uploads/2021/02/CDS-final-solution.pdf[/pdfviewer]
1. If the number 413283P759387 is divisible by 13, then what is the value of P?
(a)3
(b)6
(c)7
(d)8
If N is any number and we have to check whether N is divisibly by 13 or not. Suppose N = ( n1 n2 n3 n4 n5 n6 n7 n8 n9….)
Then N is divisible by 13, when number = ( n1 n2 n3 – n4 n5 n6 +n7 n8 n9 – ……) formed by alternative sum of blocks of 3 digits from right to left is divisible by 13.
Here N = 413283P759387 is already divisible by 13
387 – 759 + 83P – 132 + 4 = 83p – 500 which is divisible by 13
When p = 8, 83p – 500 = 838 – 500 = 338 and 338 is divisible by 13
2. What is the remainder when 2 ^1000000 is divided by 7 ?
(a)1
(b)2
(c)4
(d)6
2 ^0 = 1 ÷ 7 , rem = 1
2 ^1 = 2 ÷ 7 , rem = 2
2 ^2 = 4 ÷ 7 , rem = 4
2 ^3 = 8 ÷ 7 , rem = 1
2 ^4 = 16 ÷ 7 , rem = 2
2 ^5 = 32 ÷ 7 , rem = 4
2 ^6 = 64 ÷ 7 , rem = 1 and so on
1000000 = 2 x 500000
Therefore rem = 2
3. How many pairs of (x,y) can be chosen from the set {2,3,6,8,9} such that x/y + y/x = 2, where x≠y
(a) Zero
(b) One
(c) Two
(d)Three
x/y + y/x = 2
(x^2 +y^2)/ xy = 2
x^2 + y^2 = 2xy
x^2 + y^2 -2xy = 0
(x-y)^2 = 0
x = y
But x≠y
Ans Zero
4. Consider the pair of prime numbers (m,n) between 50 to 100 such that m-n =6. How may such pairs are there?
(a)2
(b)3
(c)4
(d)5
Prime numbers between 50 and 100
53, 59, 61, 67, 71, 73, 79, 83, 89, 97
There are 5 possible pairs: (59,53), (67,61), (73,67), (79,73), (89,83)
5.How many terms are there in the following product?
(a1+ a2 + a3)(b1 + b2 + b3 + b4)(c1 + c2 + c3 + c4 + c5)
(a)15
(b)30
(c)45
(d)60
(a1+ a2 + a3)(b1 + b2 + b3 + b4 )(c1 + c2 + c3 + c4 + c5 )
No of terms = 3 x 4 x 5 = 60
6.What is the remainder when 27 ^27 – 15 ^27 is divided by 6?
(a)0
(b)1
(c)3
(d)4
a^n – b^n is always divisible by (a-b) for all n
27 ^27 – 15 ^27 is divisible by (27 – 15) = 12 = 6 x 2
Remainder = 0
7. If a+b+c = 0, then which of the following are correct?
- a3 + b3 + c3 = 3abc
- a2 + b2 + c2 = – 2(ab + bc + ca)
- a3 + b3 + c3 = – 3ab(a+b)
Select the correct answer using the code given below.
(a) 1 and 2 only
(b) 2 and 3 only
(c) 1 and 3 only
(d)1 ,2 and 3
(i) a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
If a+b+c = 0 then
a3 + b3 + c3 – 3abc = 0
a3 + b3 + c3 = 3abc
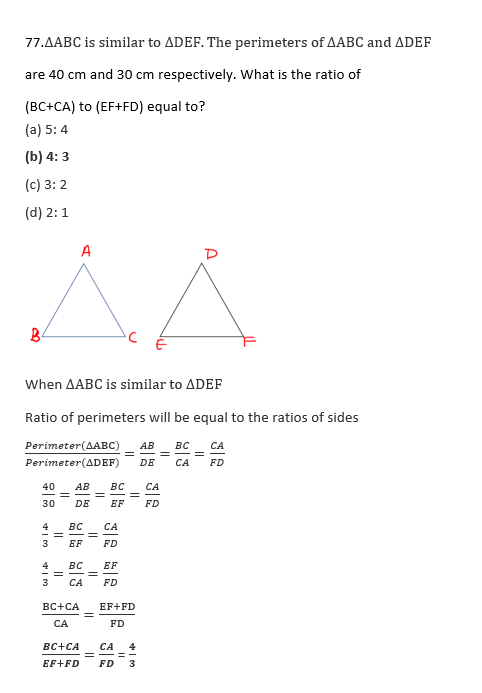
So, first statement is correct.
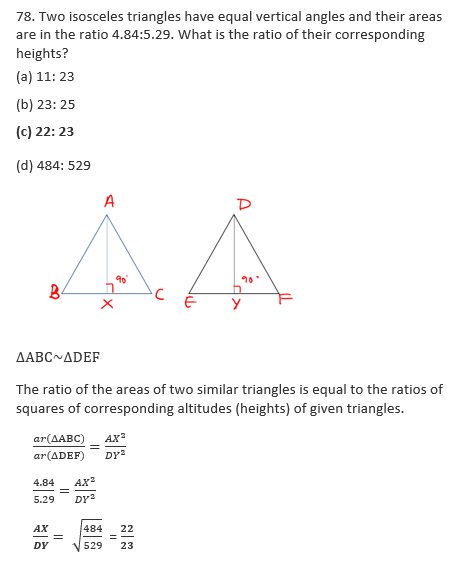
(ii)(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
If (a+ b+c) = 0
0 = a2 + b2 + c2 + 2ab + 2bc + 2ca
a2 + b2 + c2 = – 2(ab + bc + ca)
Second statement is correct.
(iii)a+b+c = 0
a+b = -c
and we know a3 + b3 + c3 = 3abc
a3 + b3 + c3 = – 3ab(a+b) ( Since a+b = -c )
Third statement is correct.
All the three statements are correct.
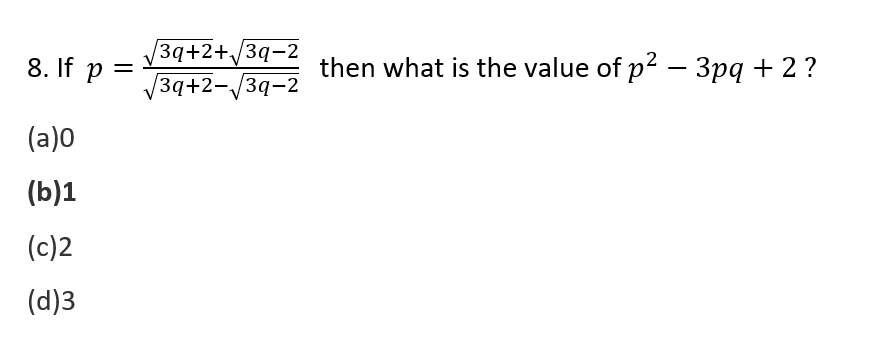

9. What is the unit digit in the expansion of 6732 ?
(a)1
(b)3
(c)7
(d)9
Cyclicity of 7 = 4 (7,9,3,1)
32 is divisible by 4. Therefore, unit digit is 1.
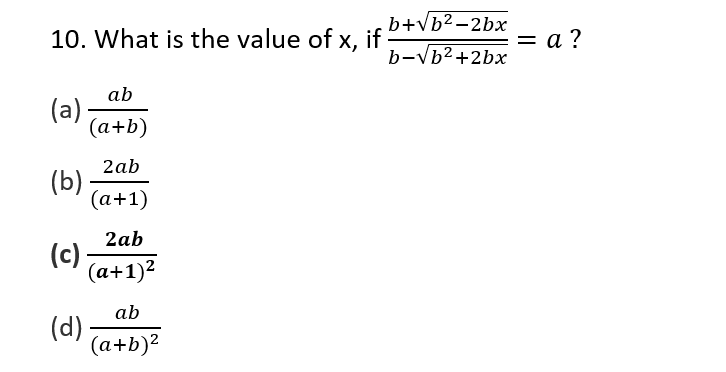

11.The expression (x3-1)(x2 – 9x + 14)/ (x2 + x +1)( x2 – 8x +7) simplifies to
(a)(x-1)
(b)(x-2)
(c)(x-7)
(d)(x+2)
(x3-1) = ( x-1)(x2 + x +1)
x2 – 9x +14 = x2 -7x – 2x +14 = x (x-7) -2(x-7) = (x-7) (x-2)
x2 – 8x +7 = x2 – 7x – x+7 = x ( x-7 ) -1 (x-7) = (x -7) (x-1)
(x3-1)(x2 – 9x + 14)/ (x2 + x +1)( x2 – 8x +7) = (x-1)(x2 + x +1)(x-7) (x-2) /(x2 + x +1)(x -7)(x-1) = (x-2)
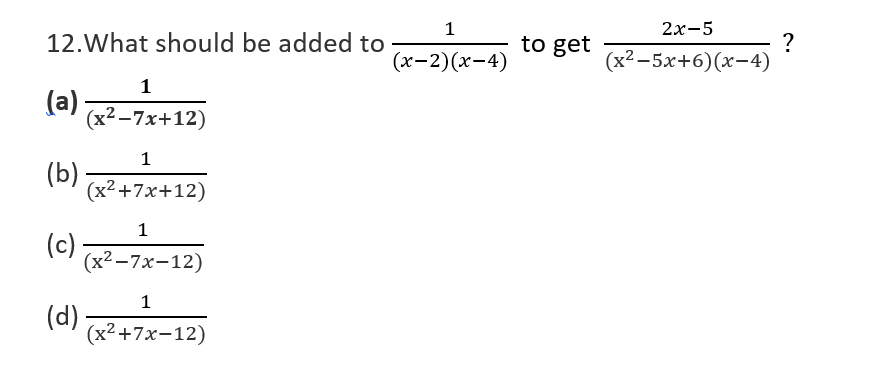
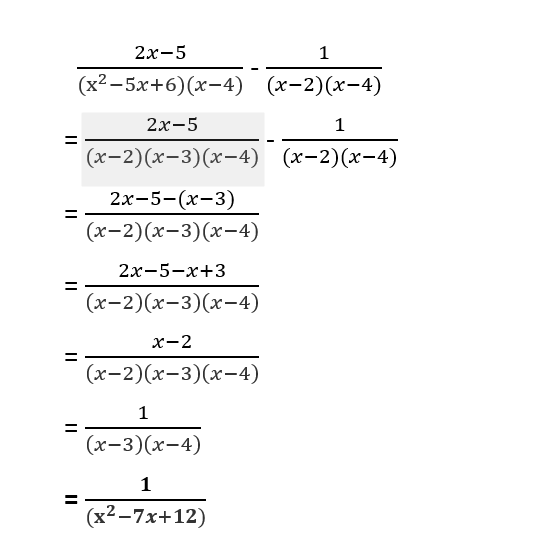

14. If (x-k) is the HCF of x2 + ax + b and x2 + cx + d, then what is the value of k?
(a) d-b / c-a
(b) d-b / a-c
(c) d+b / c+a
(d) d-b / c+a
(x-k) is factor of x2 + ax + b and x2 + cx + d
Let p(x)=x2 + ax + b and q(x) = x2 + cx + d
Then p(k) = 0 and q(k) = 0
p(k) =k2 + ak + b = 0 -(i)
q(k) = k2 + ck + d = 0 – (ii)
from (i) and (ii) we get
k2 + ak + b = k2 + ck + d
(a – c) k = d – b
k = d-b / a-c
15. Consider the following statements:
1. If x is directly proportional to z and y is directly proportional to z, then (x2 – y2) is directly proportional to z2
2. If x is inversely proportional to z and y is inversely proportional to z, then (xy) is inversely proportional to z2
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2

16. What is the HCF of x3 – 19x + 30 and x2 – 5x + 6?
(a) (x+2)(x-3)
(b) (x-2)(x+3)
(c) (x+2)(x-1)
(d)(x-3)(x-2)
x3 – 19x + 30
Put x = 0, ±1 , ±2, ±3, …… and check for which value of x, x3 – 19x + 30 = 0
When x = 2
x3 – 19x + 30 = (2)3 – 19(2) + 30 = 8 – 38 +30 = 38 – 38 = 0
By factor theorem, (x-2) is a factor of x3 – 19x + 30
x3 – 19x + 30
= x3 – 2x2 + 2x2 – 4 x – 15x + 30
= x2 (x -2) +2x (x-2) – 15 (x – 2)
= (x-2)(x2+2x -15)
= (x-2)( x2 +5 x – 3 x – 15)
=(x-2)( x(x+5)-3(x+5))
= (x-2)(x+5)(x-3)
x2 – 5x + 6
= x2 – 2x – 3x + 6
We will take x common from first 2 terms and 3 common from next two terms
= x(x – 2) – 3(x – 2)
= (x – 3)(x – 2)
HCF of x3 – 19x + 30 and x2 + 5x + 6 = (x-2)(x-3)

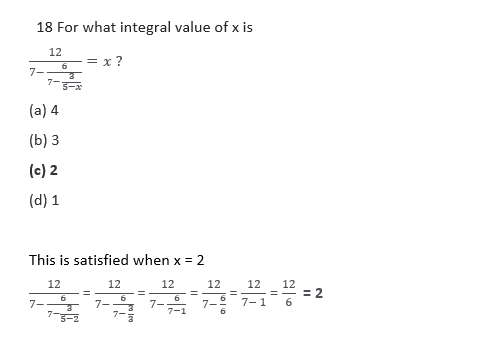
19.If x(x-1)(x-2)(x-3)+1=k2, then which one of the following is a possible expression for k?
(a) x2 – 3x + 1
(b) x2 – 3x -1
(c) x2 + 3x -1
(d) x2 – 2x -1
x(x-1)(x-2)(x-3)+1=k2
On expanding we get
x4 – 6x3 +11 x2 – 6x +1 = k2
(x2 – 3x + 1)2 = k2
k = x2 – 3x + 1








28. The incomes of A, B and C are in the ratio 7:9:12 and their expenditures are in the ratio 8:9:15. If A’s saving is one fourth of his income, then the ratio of savings of A, B and C is
(a) 56:99:69
(b) 99:56:69
(c) 69:56:99
(d) 99:69:56
Income of A, B, C are in the ratio 7: 9: 12
Let A’s income = 7x, B’s income = 9x, C’s income = 12x
Expenditures of A, B, C are in the ratio 8:9:15
Let A’s expenditure = 8y, B’s expenditure = 9y and C’s expenditure = 15y
Saving = Income – Expenditure
Then savings of A, B, C are in the ratio 7x – 8y, 9x – 9 y, 12x-15y
A’s saving is one fourth of his income (given)
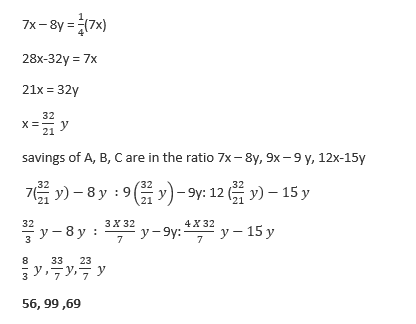
29. A train 200 m long passes a platform 100m long in 10 seconds. What is the speed of the train?
(a) 40 m/s
(b) 30 m/s
(c) 25 m/s
(d) 20 m/s

31. A trader gives successive discounts of 20%,10% and 5% respectively. What is the overall discount?
(a) 30 %
(b) 31.6%
(c) 32.8%
(d) 35%
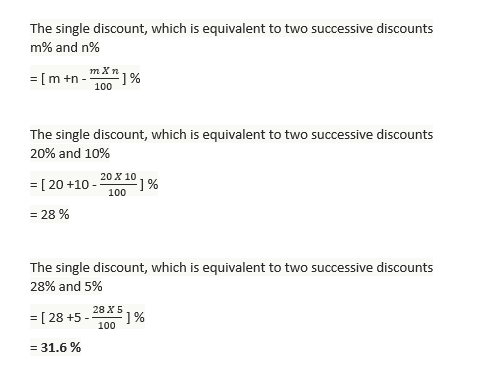
32. A sum of money was invested at simple interest at a certain rate for 5 years. Had it been invested at 5% higher rate, it would have fetched ₹500 more. What was the principal amount?
(a) ₹2,000
(b) ₹1,800
(c) ₹1,600
(d) ₹1,200
SI = P X R XT / 100
(P X (R +5) X 5 ) / 100 – (P X R X 5 )/ 100 = 500
5PR + 25 P – 5 PR = 50000
25 P = 50000
P = ₹2000
33. The difference between the compound interest (compounded annually) and the simple interest on a certain sum of money at 12% per annum for 2 years is ₹72. What is the principal amount?
(a) ₹6,500
(b) ₹6,000
(c) ₹5,500
(d) ₹5,000

34. A train travel 600 km in 5 hours and the next 900 km in 10 hours. What is the average speed of the train?
(a) 80 km/hr
(b) 90 km/hr
(c) 100 km/hr
(d) 120 km/hr

35. Walking at 4/5 th of the usual speed, a man is 12 minutes late for his office. What is the usual time taken by him to cover that distance?
(a) 48 minutes
(b) 50 minutes
(c) 54 minutes
(d) 60 minutes
Let the usual time taken by man be ‘t’ minutes and usual speed be y m/min
Here distance is same in both the cases as here the distance is between home and office.
Distance = speed x time
When he reaches office at usual time,
Distance = y X t = y t – (i)
When he is 12 minutes late for his office,
Speed = (4/5) X y
Time = t+12
Distance =(4/5) y X ( t + 12) = (4/5) y t + (48/5) y – (ii)
From (i) and (ii) we get
y t = (4/5) y t + (48/5) y
t = (4/5)t + (48/5)
t – (4/5) t = 48/5
t/5= 48/5
t = 48 minutes
36. The cost price of 100 mangoes is equal to the selling price of 80 mangoes. What is the profit percentage?
(a) 16%
(b) 20%
(c) 24%
(d) 25%
SP of 80 mangoes = x
SP of 1 mango = x /80
CP of 100 mangoes = SP of 80 mangoes = x
CP of 100 mangoes = x
CP of 1 mango = x/100
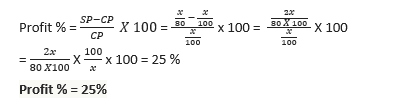
37. X sells his goods 25% cheaper than Y and 25 % dearer than Z. How much percentage is Z ‘s goods cheaper than Y?
(a) 100/3 %
(b) 40%
(c) 50%
(d) 200/3 %
We assume that Y is selling his goods for ₹100
X sells his goods 25% cheaper than Y i.e.

38. In a mixture of 80 litres of a liquid and water, 25% of the mixture is the liquid. How much water should be added to the mixture so that the liquid becomes 20 % of the mixture?
(a) 15 litres
(b) 20 litres
(c) 24 litres
(d) 25 litres
Mixture = 80 litres
Mixture contains liquid and water.
25% of the mixture is liquid = 25 % of 80 L =( 25 /100) X 80 = 20 L
Liquid = 20 litres and Water = 80 – 20 = 60 litres
According to question Liquid should become 20 % of mixture i.e.
20 % of mixture = 20 litres
(20/100) X mixture = 20
Now mixture = 100 litres
Initially mixture was 80 litres
Water added = 100 – 80 = 20 litres
39. If 20 persons can clean 20 floors in 20 days, in how many days can 16 persons clean 16 floors?
(a) 25 days
(b) 24 days
(c) 20 days
(d) 16 days
We know that
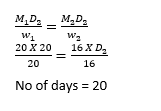
40. Let the work done by (x-1) men in (x+1) days be y. Let the work done by (x+2) men in (x-1) days be z. If y: z = 9:10, then what is the value of x?
(a) 8
(b) 9
(c) 10
(d) 12
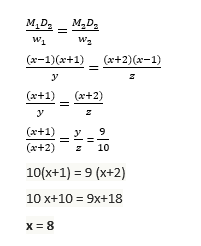
43. The sum of the reciprocals of two alternate natural numbers is 7/24 . What is the sum of the numbers?
(a) 12
(b) 13
(c) 14
(d) 16
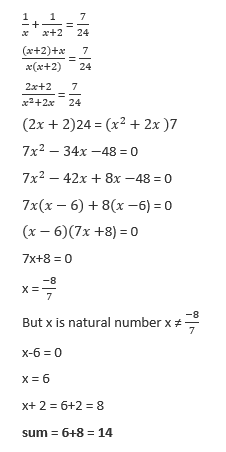

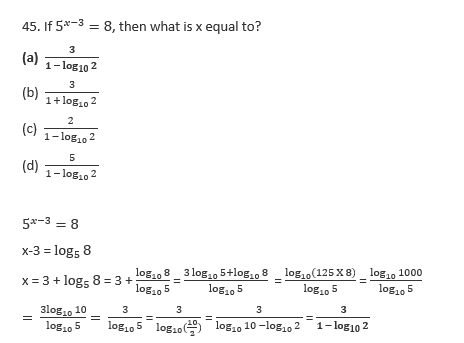
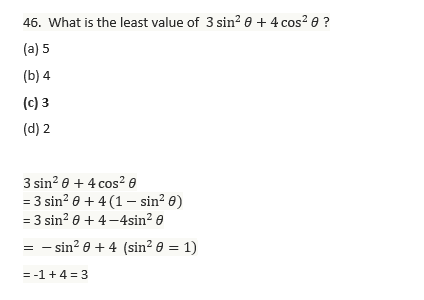



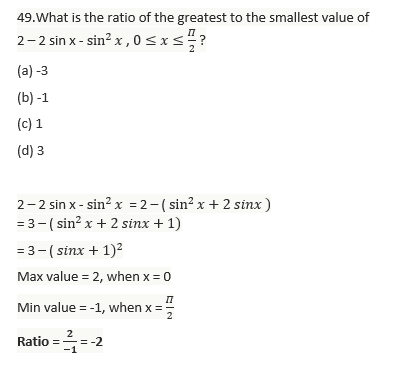



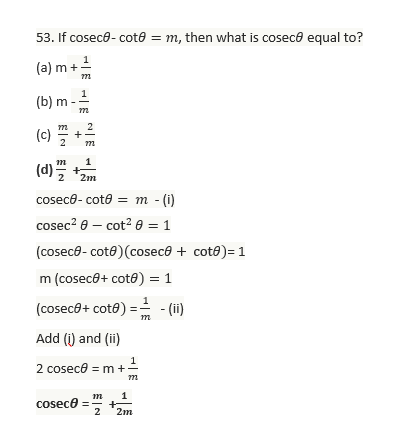
54. Let ABC be a triangle right angled at C, then what is tan A + tan B equal to?
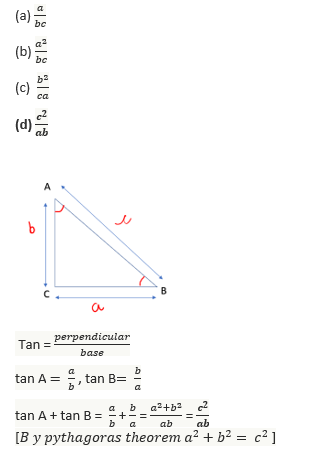




59.A pole on the ground leans at 60 with the vertical. At a point x metre away from the base of the pole on the ground, two halves of the pole subtend the same angle. If the pole and the point are in the same vertical plane, then what is the length of the pole?
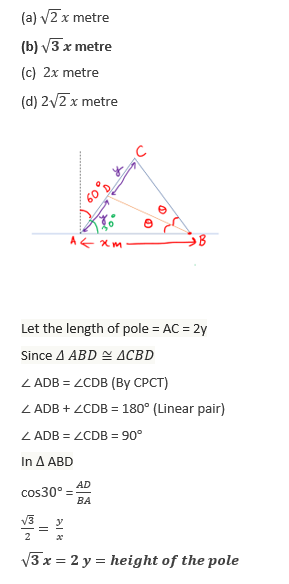
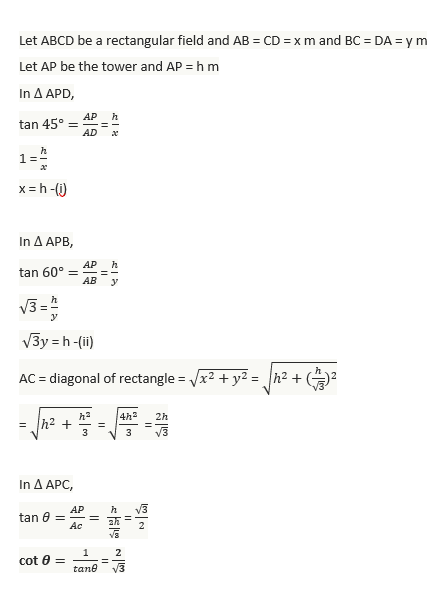
61.A cone and a hemisphere have equal bases and equal volumes. What is the ratio of the height of the cone to the radius of the hemisphere?
(a) 1:1
(b) 2:1
(c) 3:2
(d) 4:3
Let the height of the cone be h.
Since cone and hemisphere have same base i.e., radius of cone and hemisphere are equal.
Let r be the radius of cone and hemisphere
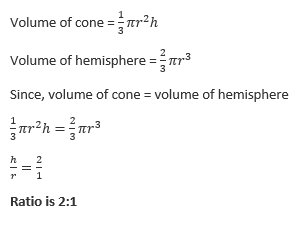
62. A solid sphere of diameter 60 mm is melted to stretch into a wire of length 144cm. What is the diameter of wire?
(a) 0.5 cm
(b) 1 cm
(c) 1.5 cm
(d) 2 cm
Diameter of sphere = 60 mm = 6cm
Radius of sphere = R = 3 cm
Length of wire = h = 144 cm
Solid sphere is recast into wire so
Volume of sphere = Volume of wire (cylinder)
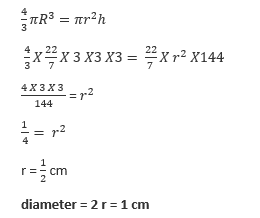
63.The ratio of the radius of base to the height of a cylinder is 2:3. If the volume of the cylinder is 1617 ![]() then what is the curved surface area of the cylinder?
then what is the curved surface area of the cylinder? ![]()


Height of cylindrical pipe = 14cm
Inner radius = r
Outer radius = R

65. A metal solid cube of edge 24 cm is melted and made into three small cubes. If the edge of two small cubes are 12 cm and 16 cm, then what is the surface area of the third small cube?

66. A conical vessel whose internal radius is 5cm and height is 24cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10cm. What is the height to which water rises?
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
Height of cone = H = 24cm
Radius of cone = R = 5 cm
Radius of cylinder = r = 10 cm
Water from conical vessel is emptied into cylindrical vessel
Volume of cone = Volume of cylinder
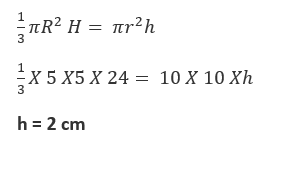
67. A metal solid cube of side 22 cm is melted to make a cone of height 21 cm. What is the radius of the base of the cone? ![]()
(a) 11 cm
(b) 16.5 cm
(c) 22 cm
(d) 27.5 cm
Side of metal solid cube = a = 22cm
Height of cone = h = 21 cm
A metal slid cube is recast into cone
Volume of cube = Volume of cone
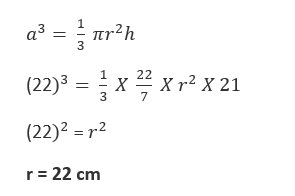

Height of cone = h = 24 cm

69. A rectangular paper is 44cm long and 22 cm wide. Let x be the volume of the largest cylinder formed by rolling the paper along its length and y be the volume of the largest cylinder formed by rolling the paper along its width. What is the ratio of x to y? ![]()
(a) 1:1
(b) 2:1
(c) 1:2
(d) 3:2
Length of paper = 44cm
Width of paper = 22cm
Let x be the volume of the largest cylinder formed by rolling the paper along its length
height of cylinder = 22 cm
circumference of circle = length of paper


71.A cloth of 3m width is used to make a conical tent 12m in diameter with a slant height of 7m. What is the length of the cloth? ![]()
(a) 21 m
(b) 28 m
(c) 44 m
(d) 66 m
Curved surface area of cone = Area of cloth
Slant height = 7 m
Diameter = 12m
Radius = 6m
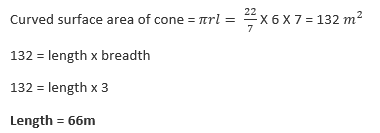
72. A sphere of diameter 6cm is dropped into a cylindrical vessel partly filled with water. The radius of the vessel is 6 cm. If the sphere is completely submerged in water, then by how much will the surface level of water be raised?
(a) 0.5 cm
(b) 1 cm
(c) 1.5 cm
(d) 2 cm
Diameter of sphere = 6 cm
r = radius of sphere = 3 cm
R = radius of cylindrical vessel = 6 cm
Let level of water raised be h cm
Volume of water raised in the cylindrical vessel = Volume of sphere
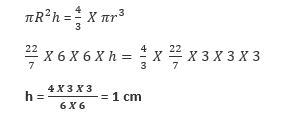
73. A sector is cut from the circle of radius 21 cm. If the length of the arc of the sector is 55cm, then what is the area of sector?

74. A wire is in the form of a circle of radius 70 cm. If it is bent in the form of a rhombus, then what is its side length? ![]()
(a) 55 cm
(b) 75 cm
(c) 95 cm
(d) 110 cm
Perimeter of circle = Perimeter of rhombus

75. If the perimeter of a semi-circular park is 360m, then what is its area? ![]()
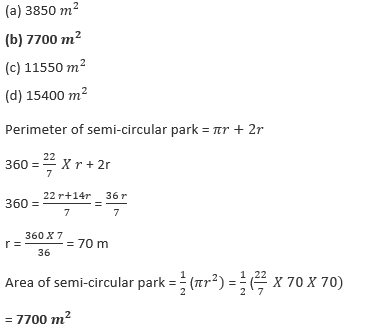
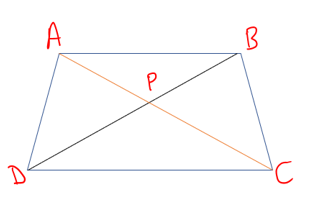
76. In a trapezium ABCD, AB is parallel to DC. The diagonals AC and BD intersect at P. If AP: PC = 4:(4x-4) and BP:BD = (2x-1) :(2x+4), then what is the value of x?
(a) 4
(b) 3
(c) 3/2
(d) 2
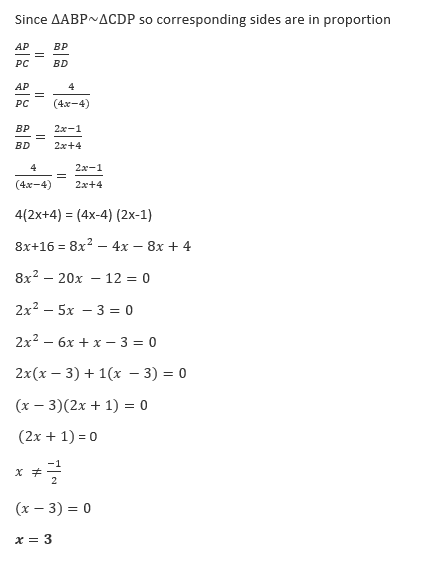
79. ABC is a triangle right angled at A and AD is perpendicular to BC. If BD = 8 cm and DC =12.5 cm, then what is AD equal to?
(a) 7.5 cm
(b) 8.5 cm
(c) 9 cm
(d) 10 cm

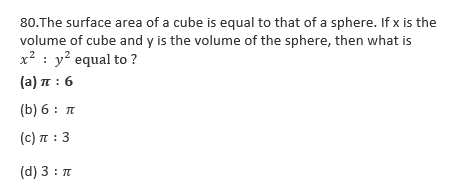
Let a be the side of cube and r be the radius of sphere.
Surface area of cube = Surface area of sphere
81.The sides of a right- angled triangle are in the ratio x : (x-1): (x-18) . What is the perimeter of the triangle?
(a) 28 units
(b) 42 units
(c) 56 units
(d) 84 units

82. ABC is a triangle right angled at B. Let M and N be two points on AB such that AM = MN = NB. Let P and Q be two points on AC such that PM is parallel to QN and QN is parallel to CB. If BC = 12cm, then what is (PM+QN) equal to?
(a) 10 cm
(b) 11 cm
(c) 12 cm
(d) 13cm

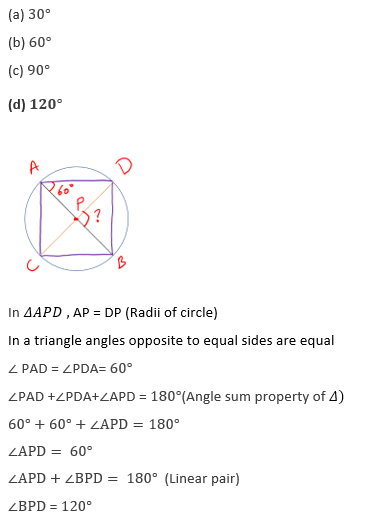
83. AB and CD are the diameters of a circle which intersects at P. Join AC, CB, BD and DA. If ∠PAD = 60 ,then what is ∠BPD equal to?
84. An equilateral triangles ABC and a scalene triangle DBC are inscribed in a circle on same side of the arc. What is ∠BDC equal to?
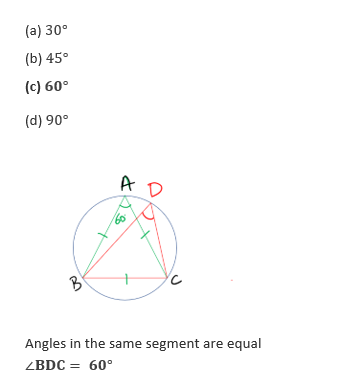
85. The sides of a triangle ABC are 4 cm, 6cm and 8cm. With the vertices as centres, three circles are drawn each touching the other two externally. What is the sum of the radii of three circles?
(a) 6 cm
(b) 7 cm
(c) 9 cm
(d) 10 cm
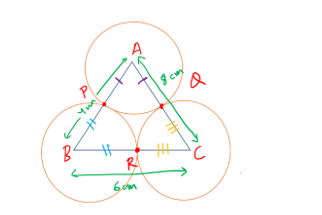
Since AP = AQ (Radii of circle)
BP = BR (Radii of circle)
CR =CQ (Radii of circle)
Let AP = AQ = a then, BP = AB – AP = 4 – a = BR
CR = BC – BR = 6 – (4-a) = 2 +a = CQ
Since AC = AQ+QC
8 = a + 2 +a
6 = 2a
a = 3
AP = AQ = a = 3cm
BP = BR = 4 – a = 4-3 = 1cm
CR = CQ = 2+a = 2+3 = 5cm
Sum of three radii = AP+BP+CR = 3+1+5 = 9 cm
86. Let PAB be a secant to a circle intersecting the circle at A and B. Let PT be the tangent segment. If PA = 9 cm and PT =12cm, then what is AB equal to?
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) 9 cm
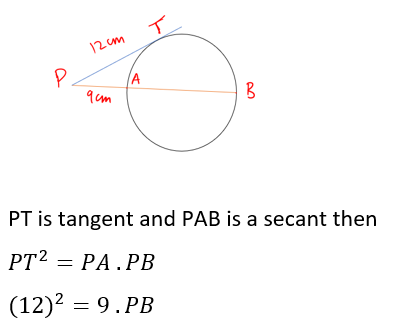
144 = 9. PB
PB = 16 cm
AB = PB – PA = 16-9 = 7 cm
87.If the perimeter of right-angled triangle is 30cm and the hypotenuse is 13cm, then what is the area of the triangle?

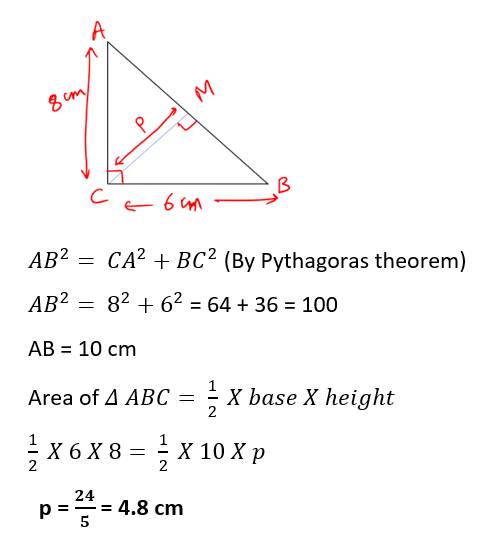
88. ABC is a triangle right angled at C. Let p be the length of the perpendicular drawn from C on AB. If BC = 6cm and CA = 8 cm, then what is the value of p?
(a) 5.4 cm
(b) 5 cm
(c) 4.8 cm
(d) 4.2 cm
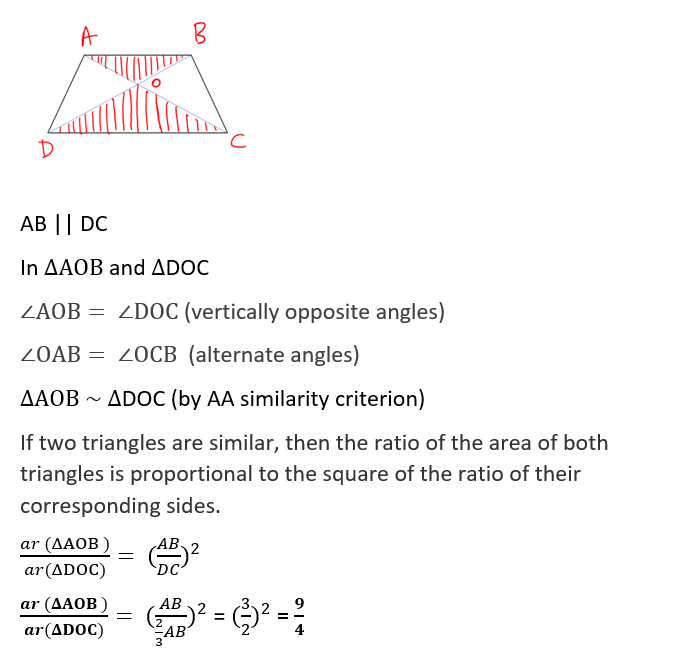
89. ABCD is a trapezium in which AB is parallel to DC and 2AB = 3DC. The diagonals AC and BD intersect at O. What is the ratio of the area of △AOB to that of △DOC?
(a) 2: 1
(b) 3: 2
(c) 4: 1
(d) 9: 4
90. A circle touches all the four sides of a quadrilateral ABCD. If AB = 9cm, BC = 8 cm and CD = 12cm, then what is DA equal to?
(a) 14 cm
(b) 13 cm
(c) 12 cm
(d) 11 cm
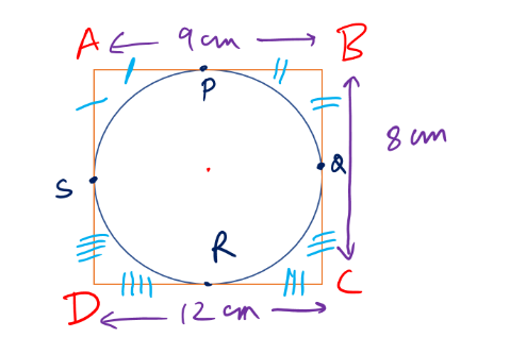
AP = AS (Tangent drawn from an external point A)
BP = BQ (Tangent drawn from an external point B)
CQ = CR (Tangent drawn from an external point C)
DR = DS (Tangent drawn from an external point D)
Let AP = AS = x
Then BP = AB – AP = 9 – x = BQ
CQ = BC – BQ = 8 – (9-x) = x-1= CR
DR = CD – CR = 12 – (x-1) = 13 – x = DS
DA = AS +DS = x + 13-x = 13 cm
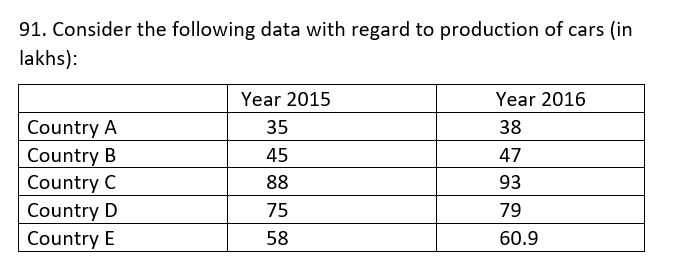
In which of the countries, the production of cars has increased by more than or equal to 5 % in 2016 over 2015?
(a) B and C
(b) A, C and D only
(c) A, C, D and E
(d) A, D and E only

Production of cars has increased by more than or equal to 5% in 2016 over 2015 in Countries A, C, D and E.
92. The following table shows the marks of 90 students in a test of 80 marks:
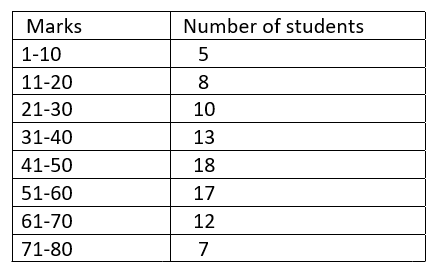
The percentage of students who have obtained less than or equal to 50% marks is
(a) 30 %
(b) 40 %
(c) 45 %
(d) 60 %

93. What is the median of the following data?
2,3,-1,2,6,8,9
(a) 2
(b) 3
(c) 4
(d) 5
Firstly, we will arrange these numbers in ascending order
-1,2,2,3,6,8,9
The middle value is 3. So median = 3
94. What is the arithmetic mean of first ten composite numbers?
(a) 8.5
(b) 9.5
(c) 10.2
(d) 11.2
4,6,8,9,10,12,14,15,16,18 are first 10 composite numbers

95. The marks obtained by 5 students are 21,27,19,26,32. Later on 5 grace marks are added to each student. What are the average marks of the revised marks of the students?
(a) 26
(b) 30
(c) 31
(d) 32

96. Let p be the mean of m observations and q be the mean of n observations, where p ≤ q. If the combined mean of (m+n) observations is c, then which one of the following is correct?
(a) c ≤ p
(b) c ≥ q
(c) p ≤ c ≤ q
(d) q ≤ c ≤ p
p ≤ q (given)
p≤ c ≤ q
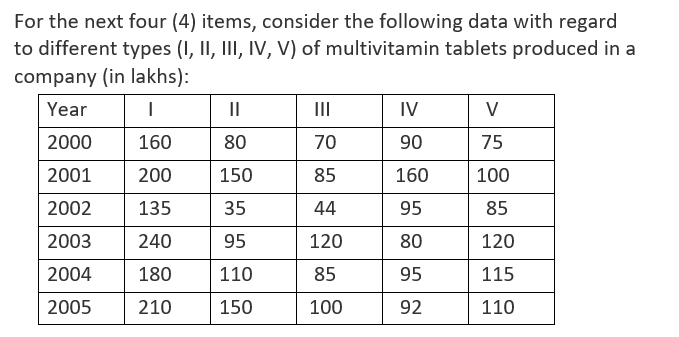
97. Which product is produced least over the years 2000 – 2005?
(a) Type II
(b) Type III
(c) Type IV
(d) Type V
Production of tablet I (2000-2005)
=160+200+135+240+180+210 =1125
Production of tablet II (2000-2005)
=80+150+35+95+110+150 = 620
Production of tablet III (2000-2005)
= 70+85+44+120+85+100 =504
Production of tablet IV (2000-2005)
=90+160+95+80+95+92 = 612
Production of tablet V (2000-2005)
= 75+100+85+120+115+110 = 605
Type III is produced least over the years 2000-2005
98. In which one of the following pairs of years, the difference in total number of tablets produced between them is minimum?
(a) (2003, 2005)
(b) (2001, 2005)
(c) (2003, 2004)
(d) (2000, 2002)
For year 2000, production= 160+80+70+90+75 = 475
For year 2001, production = 200+150+85+160+100= 695
For year 2002, production = 135+35+44+95+85 = 394
For year 2003, production = 240+95+120+80+120 = 655
For year 2004, production = 180+110+85+95+115 = 585
For year 2005, production = 210+150+100+92+110 =662
Difference in the total production between 2003 and 2005 = 655- 662 = 7
99. The ratio of the percentage drop in total production in 2004 compared to 2001 to that in 2000 compared to 2001, is
(a) 1/3
(b) 1/4
(c) 1/2
(d) 1/5
Difference in the total production of 2004 and 2001
= 695 – 585 = 110
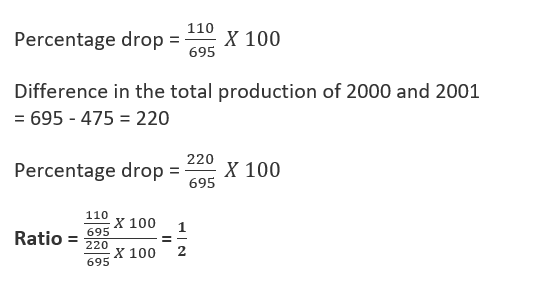
100. In which year, the production of Type I is more than the sum of the production of Type III and Type IV?
(a) 2001
(b) 2002
(c) 2003
(d) 2004
In year 2003, Type I production = 240 and (Type III+ Type IV) Production = 120 + 80 = 200
240 > 200