Full detailed solution of NDA Maths Exam 2021. NDA exam for Army, Navy and Air Force wings . National Defence Academy conducted twice a year. If you have any questions, please write in the comment section.

2. The value of x, satisfying the equation log cosx sinx = 1, where 0 < x < π/2, is
(a) π/12
(b) π/3
(c) π/4
(d) π/6
log cosx sinx =
log sinx = log cosx
This is possible when x = π/4

4. If C0 , C1 , C2 ,…. , Cn are the coefficients in the expansion of (1 + x )n, then what is the value of C1 + C2 +…. +Cn ?
(a) 2 n
(b) 2 n – 1
(c) 2 n-1
(d) 2 n – 2
Since nC0 + nC1 + nC2 + …. + nCn = 2 n
1 + nC1 + nC2 +…. + nCn = 2 n
nC1 + nC2 +…. + nCn = 2 n – 1
5. If a + b + c = 4 and ab + bc + ca = 0, then what is the value of the following determinant?

= 4 [ 1 ((c-b)(b-c) – (a-b)(a-c)) + 0 + 0]
= 4 [ cb – c 2 – b 2 + bc – ( a 2 – ac – ba +bc)]
= 4 [ – a 2 – b 2 – c 2 + ab + bc + ca ]
= – 4( a 2 + b 2 + c 2 )
= – 4( (a + b + c) 2 -2ab – 2bc -2ca )
= -64
6. The number of integer value of k, for which the equation 2sinx = 2k +1 has a solution, is
(a) zero
(b) one
(c) two
(d) four
2sinx = 2k +1
Sin x = (2k+1)/2
Since sin x lies between -1 and 1
-1 ≤ (2k+1)/2 ≤ 1
-2 ≤ 2k+1 ≤ 2
-3 ≤ 2k ≤ 1
-1.5 ≤ k ≤ 0.5
K can be -1 or 0
There are two integer values of k.
7. If a1 , a2 , a3 , ….. a9 , are in GP, then what is the value of the following determinant ?
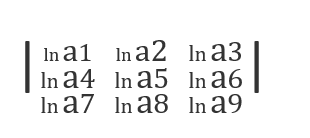
(a) 0
(b) 1
(c) 2
(d) 4
a1 , a2 , a3 , ….. a9 , are in GP
If a1= a
Then a2 = a 2 , ………., a9 = a 9
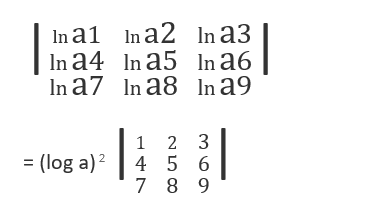
= (log a) 2 x 0
= 0
8. If the roots of quadratic equation x 2 + 2x + k = 0 are real, then
(a) k < 0
(b) k ≤ 0
(c) k < 1
(d) k ≤ 1
Root are real when discriminant ≥ 0
b 2 – 4ac ≥ 0
(2) 2 – 4k ≥ 0
4 – 4k ≥ 0
1 ≥ k
K ≤ 1
9. If n = 100! , then what is the value of the following?
[1/ log 2 n ] + [1/ log 3 n ] + [1/ log 4 n ] + …+ [1/ log 100 n ]
(a) 0
(b) 1
(c) 2
(d) 3
[1/ log 2 n ] + [1/ log 3 n ] + [1/ log 4 n ] + …+ [1/ log 100 n ]
[ 1/ log a b = log b a ]
= log n 2 + log n 3 + log n 4 + …+ log n 100
[ log a b + log a c = log a bc ]
= log n ( 2 x 3 x 4 x… x 100)
= log n (100!) [ n = 100 !]
= log n n
= 1
10. If z = 1 + i, where i = √ -1 , then what is modulus of Z + 2/Z ?
(a) 1
(b) 2
(c) 3
(d) 4
Z + 2 /Z
= 1 + i + ( 2 / 1+i)
= ( 2i + 2 ) / 2
= 2
Modulus = 2
11. If A and B are two matrices such that AB is of order n x n, then which of the following is correct?
(a) A and B should be square matrices of same order.
(b) Either A or B should be a square matrices.
(c) Both A and B should be of same order.
(d) Orders of A and B need not be the same.
12. How many matrices of different orders are possible with elements comprising all prime numbers less than 30?
(a) 2
(b) 3
(c) 4
(d) 6
Prime numbers less than 30: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
Total Prime no’s less than 30 = 10
Possible orders: 10 x 1, 2 x 5, 5×2, 1 x10
13. Let
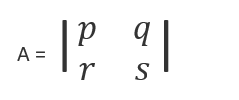
where p, q, r and s are any four different prime numbers less than 20. What is the maximum value of the determinant?
(a) 215
(b) 311
(c) 317
(d) 323
Prime numbers less than 20: 2, 3, 5, 7, 11, 13, 17, 19
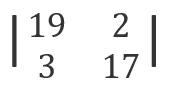
= 19 x 17 – 2 x 3
= 323 – 6
= 317
14. If A and B are square matrices of order 2 such that det(AB) = det(BA), then which of the following is correct?
(a) A must be a unit matrix.
(b) B must be a unit matrix.
(c) Both A and B must be unit matrices.
(d) A and B need not be unit matrices.
15. What is cot2x cot4x – cot4x cot6x – cot6x cot2x equal to?
(a) -1
(b) 0
(c) 1
(d) 2
cot2x cot4x – cot4x cot6x – cot6x cot2x
= cot2x cot4x – cot6x (cot4x + cot2x)
= cot2x cot4x – cot (4x+2x)(cot4x + cot2x)
[ cot (a+b) = (cota cotb -1)/ cosa + cotb ]
= cot2x cot4x – (cot4x cot2x – 1)
= cot2x cot4x – cot4x cot2x + 1
= 1
16. If tan x = -3/4 and x is in the second quadrant, then what is the value of sinx . cosx?
(a) 6/25
(b) 12/25
(c) -6/25
(d) -12/25
Since tan x = -3/4
Sinx = -3/5 , cosx = 4/5
Sinx . cosx = -3/5 x 4/5 = -12/25
17. What is the value of the following?
Cosec(7π/6) sec(5π/3)
(a) 4/3
(b) 4
(c) -4
(d) -4/√ 3
Cosec(7π/6) sec(5π/3)
= Cosec(π + π/6) sec(2π – π/3)
= – Cosec(π/6) sec( π/3)
= – 2 x 2
= -4
18. If the determinant
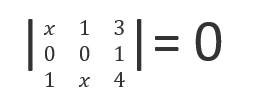
then what is x equal to?
(a) – 2 or 2
(b) -3 or 3
(c) -1 or 1
(d) 3 or 4
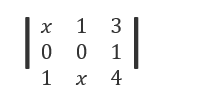
= 0 (4-3x) + 0(4x-3) -1 (x 2 -1)
= – x 2 + 1
Since determinant = 0
– x 2 + 1 = 0
x = -1 or +1
19. What is the value of the following?
tan31 tan 33 tan35 …..tan57 tan59
(a) -1
(b) 0
(c) 1
(d) 2
tan31 tan 33 tan35 ….tan44 tan45 tan46….tan57 tan59
= tan(90-59) tan (90-57) tan (90-55) ….tan(90-46) tan45 tan46….tan57 tan59
= cot59 cot57 cot55 ….cot46 tan45 tan46….tan57 tan59
= 1 [ tanx = 1/cotx ]
20. If
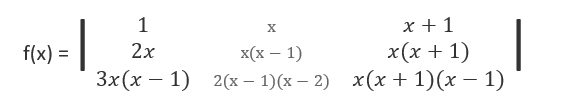
then what is f(-1) + f(0) + f(1) equal to ?
(a) 0
(b) 1
(c) 100
(d) -100

Similarly f(0) = 0 and f(1) = 0.
Therefore, f(-1) + f(0) + f(1) = 0
21. The equation sin-1 x – cos-1 x = π/6 has
(a) no solution
(b) unique solution
(c) two solutions
(d) infinite number of solutions
sin-1 x – cos-1 x = π/6
we know, sin-1 x + cos-1 x = π/2
sin-1 x – (π/2 – sin-1 x) = π/6
2 sin-1 x – π/2 = π/6
2 sin-1 x = π/6 + π/2 = 2π/3
sin-1 x = π/3
This equation has unique solution.
22. What is the value of the following?
(sin 24 + cos 66) (sin24 – cos66)
(a) -1
(b) 0
(c) 1
(d) 2
(sin 24 + cos 66) (sin24 – cos66)
= sin224 – cos2 66
= sin2(90 – 66) – cos2 66
= cos266 – cos2 66
= 0
23. A chord subtends an angle 120 at the centre of a unit circle. What is the length of the chord?
(a) √2 -1 units
(b) √3 – 1 units
(c) √2 units
(d) √3 units
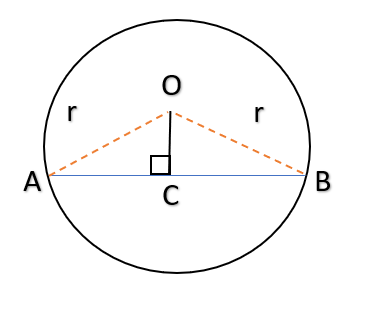
Let AB be a chord and angle AOB = 120°
AO = OB = radius = 1 unit
OC is perpendicular to AB
Perpendicular from the centre to a chord bisects the chord OC
In triangle AOC
Sin60° = AC/AO
√3/2 = AC /1
AC = √3/2
2AC = √3
AB = √3 units
So, chord length = √3 units
24. What is (1 + cot θ – cosec θ) (1 + tan θ + sec θ) equal to?
(a) 1
(b) 2
(c) 3
(d) 4
(1 + cot θ – cosec θ) (1 + tan θ + sec θ)
= (1 + [cos θ/sin θ] – [1/sin θ]) (1 + [sin θ/ cos θ] + [1/cos θ])
= [( sin θ + cos θ -1)/ sin θ ] [( cos θ + sin θ + 1)/ cos θ ]
= ( sin θ + cos θ)2 -1 / sin θ cos θ
= 2sin θ cos θ/ sin θ cos θ
= 2
25. What is
(1 + tan 2 θ / 1 + cot 2 θ) – (1 – tan θ / 1 – cot θ) 2
equal to?
(a) 0
(b) 1
(c) 2 tan θ
(d) 2 cot θ
(1 + tan 2 θ / 1 + cot 2 θ)
= sec 2 θ / cosec2 θ
= sin 2 θ / cos2 θ
= tan 2 θ
(1 – tan θ / 1 – cot θ) 2
= (1 – tan θ / 1 – (1/tan θ) 2
= tan 2 θ
Therefore, (1 + tan 2 θ / 1 + cot 2 θ) – (1 – tan θ / 1 – cot θ) 2 = 0
26. What is the interior angle of a regular octagon of side length 2 cm?
(a) π/2
(b) 3π/4
(c) 3π/5
(d) 3π/8
Each exterior angle of the regular octagon = 2 π /8 = π/4
interior angle of the regular octagon = π – π/4 = 3π/4
27. If 7 sin θ + 24 cos θ = 25, then what is value of (sin θ + cos θ)?
(a) 1
(b) 26/25
(c) 6/5
(d) 31/25
7 sin θ + 24 cos θ = 25
7 (7/25) + 24 (24/25) = 25
Therefore, sin θ = 7/25 and cos θ = 24/25
(sin θ + cos θ) = 7/25 +24/25
= 31/25
28. A ladder 6 m long reaches a point 6 m below the top of a vertical flagstaff. From the foot of the ladder, the elevation of the top of the flagstaff is 75. What is the height of the flagstaff?
(a) 12m
(b) 9m
(c) (6 + √3) m
(d) (6 + 3√3) m
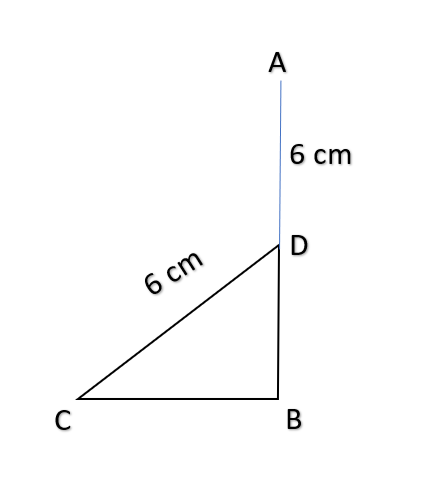
AD = CD = 6m
Angle DCB = 75°
Height of Flagstaff = AD + DB
In △CBD,
Sin75°= DB/CD
√3/2 = DB/6
DB = 3√3
Height of Flagstaff = AD + DB = (6 + 3√3) m
29. The shadow of a tower is found to be x metre longer, when the angle of elevation of the sun changes from 60 to 45. If the height of the tower is 5(3+ √3) m, then what is x equal to?
(a) 8 m
(b) 10 m
(c) 12 m
(d) 15 m
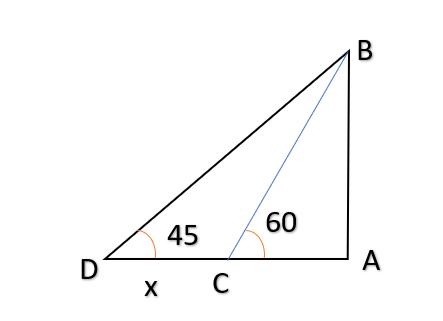
5 (3+ √3) = AB = the height of tower
In △ ABD
tan 45 = AB/AD
1 = 5 (3+ √3) /AD
AD = 5 (3+ √3)
AD = AC + CD = AC + x
5 (3+ √3) = AC + x
AC = 5 (3+ √3) – x
In △ ABC
tan 60 = AB/ AC
√3 = 5 (3+ √3) / 5 (3+ √3)– x
15√3 + 15 – √3x = 15 + 5√3
10√3 = √3x
x = 10m
30. If 3 cos θ = 4 sinθ, then what is the value of tan (45+θ) ?
(a) 10
(b) 7
(c) 7/2
(d) 7/4
Since 3 cos θ = 4 sinθ
tanθ = 3/4
tan (45+θ) = (tan45 + tanθ) / (1 – tan45tanθ)
= (1+ 3/4) / (1 – 1 x 3/4)
= 7/4 x 4
= 7
31. tan -1 x + cot -1 x = π/2 holds, when
(a) x ∈ R
(b) x ∈ R – (-1,1) only
(c) x ∈ R – {0} only
(d) x ∈ R- [-1,1] only
32. If tan A = 1/7, then what is cos2A equal to?
(a) 24/25
(b) 18/25
(c) 12/25
(d) 6/25
Cos2A = (1 – tan 2 A) / (1 + tan 2 A)
= (1 – 1/49) / (1 + 1/49)
= 48 / 50
= 24 / 25
34. What is the area of the triangle ABC with sides a = 10cm, c = 4cm and angle B = 30 ?
(a) 16 cm 2
(b) 12 cm 2
(c) 10 cm 2
(d) 8 cm 2
Area of triangle = (1/2) x ac sinB
= (1/2) x 10 x 4 x (1/2)
= 10 cm 2
35. Consider the following statements:
1. A = {1,3,5} and {2,4,7} are equivalent sets.
2. A = {1,5,9} and {1,5,5,9, 9} are equal sets.
Which of the above statements is/ are correct?
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2
Both statements are correct.
In equivalent sets, cardinality of both the sets are same.
36. Consider the following statements:
1. The null set is a subset of every set.
2. Every set is a subset of itself.
3. If a set has 10 elements, then its power set will have 1024 elements.
Which of the above statements are correct?
(a) 1 and 2 only
(b) 2 and 3 only
(c) 1 and 3 only
(d) 1, 2 and 3
All statements are correct.
37. Let R be a relation defined as xRy if and only if 2x + 3y = 20, where x, y ∈ N. How many elements of the form (x,y) are there in R?
(a) 2
(b) 3
(c) 4
(d) 6
There are 3 elements (1,6) , (4,4), (7,2) in R.
38. Consider the following statements:
1. A function f : Z ⇒ Z, defined by f(x) = x+1, is one – one as well as onto.
2. A function f : N ⇒ N, defined by f(x) = x+1, is one – one as well as onto.
Which of the above statements is/ are correct?
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2
Both the statements are correct.
39. Consider the following in respect of a complex number Z:
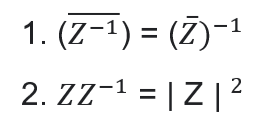
Which of the above statements is/ are correct?
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2
40. Consider the following statements in respect of an arbitrary complex number Z:
1. The difference of Z and its conjugate is an imaginary number.
2. The sum of Z and its conjugate is a real number.
Which of the above statements is/ are correct?
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2
42. If α and β are the roots of the equation 4x2 + 2x -1= 0, then which one of the following is correct?
(a) β = – 2 α 2 – 2 α
(b) β = 4α 2 – 3α
(c) β = α 2 -3 α
(d) β = – 2 α 2 + 2 α
Since β is the roots of 4x2 + 2x -1= 0. Therefore, it will satisfy 4x2 + 2x -1= 0
We get,
4 β 2 + 2 β -1= 0
2 β = 1 – 4 β 2 – (i)
Since α and β are the roots of 4x2 + 2x -1= 0
Sum of roots = α + β = -b/a = -2/4 = -1/2
α + β = -1/2
β = – α – ½
Put β = – α – ½ in equation (i)
2 β = 1 – 4(- α – ½) 2
On solving we get, β = – 2 α 2 + 2 α
43 If one root of 5x2 + 26x + k = 0 is reciprocal of the other, then what is the value of k?
(a) 2
(b) 3
(c) 5
(d) 8
Let one root be a and other root be 1/a
Sum of root = a + 1/a = -b/a = 26/5
Product of root = a x 1/a = c/a = k /5
1 = k/5
k = 5
44. In how many ways can a team of 5 players be selected from 8 players so as not to include a particular player?
(a) 42
(b) 35
(c) 21
(d) 20
Particular player is not added
No. of ways = 7C5
= 7! / 5! 2!
= 7 x 3 = 21
45. What is the coefficient of the middle term in the expansion of (1 + 4x + 4x2)5 ?
(a) 8064
(b) 4032
(c) 2016
(d) 1008
(1 + 4x + 4x2)5
= ((1 + 2x)2)5
= (1 + 2x)10
Middle term = 10C5 (1)5 (2x)5
Coefficient = 10C5 (2)5
= 252 x 32
= 8064
46. What is C(n,1) + C(n,2) + … + C(n,n) equal to ?
(a) 2 + 22 + 23 +…. + 2n
(b) 1 + 2 + 22 + 23 + …. + 2n
(c) 1 + 2 + 22 + 23 + …. + 2n-1
(d) 2 + 22 + 23 +…. + 2n-1
Since C(n,0) + C(n,1) + C(n,2) + … + C(n,n) = 2n
C(n,1) + C(n,2) + … + C(n,n) = 2n – 1
Since 1, 2, 22, 23, …., 2n-1 are terms of a gp
Sum = 1(2n-1) / 2-1
= 2n – 1
47. What is the sum of the coefficients of first and last terms in the expansion of (1+x)2n, where n is a natural number?
(a) 1
(b) 2
(c) n
(d) 2n
Coefficient of first term = 2nC0 = 1
Coefficient of last term = 2nC2n =1
Sum of coefficients of first and last terms = 2
48. If the first term of an AP is 2 and the sum of the first five terms is equal to one fourth of the sum of the next five terms, then what is the sum of first ten terms?
(a) -500
(b) -250
(c) 500
(d) 250
Here a = first term = 2
S5 = 1/4(S10 – S5 )
Therefore, 5S5 = S10
5 [ 5/2( 2 x 2 + (5-1)d ] = [ 10/2( 2 x 2 + (10-1)d ]
25/2 [ 4 + 4d] = 5 [ 4 + 9d]
5 [ 2 + 2d] = 4 + 9d
10 + 10d = 4 + 9d
d = -6
S10 =10/2[ 2 x 2 + (10-1) x -6]
= 5 [ 4 -54]
= 5 x -50
= -250
49. Consider the following statements
1. If each term of a GP is multiplied by same non zero number, then the resulting sequence is also a GP.
2. If each term of a GP is divided by same non zero number, then the resulting sequence is also a GP.
Which of the above statements is/ are correct?
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2
Both statements are correct
50. How many 5 digit prime numbers can be formed using the digits 1,2,3,4,5 if the repetition of digits is not allowed?
(a) 5
(b) 4
(c) 3
(d) 0
Not possible
51. If f(x+1) = x2 – 3x + 2, then what is f(x) equal to?
(a) x2 – 5x + 4
(b) x2 – 5x + 6
(c) x2 + 3x + 3
(d) x2 – 3x + 1
f(x+1) = x2 – 3x + 2,
Replace x by x -1
f((x-1)+1) = (x-1)2 – 3(x-1) + 2
f(x) = x2 – 2x + 1 – 3x + 3 + 2
f(x) = x2 – 5x + 6
52. If x2 , x , -8 are in AP, then which one of the following is correct?
(a) x {-2}
(b) x {4}
(c) x {-2, 4}
(d) x {-4,2}
2 x = x2 – 8
x2 – 2x – 8 = 0
(x – 4)(x+2) = 0
x = -2 , 4
53. The third term of a GP is 3. What is the product of its first five terms?
(a) 81
(b) 243
(c) 729
(d) Cannot be determined due to insufficient data
Third term is 3
Let common ratio be r. Then, first 5 terms of GP are in the form 3 /r2, 3 /r , 3, 3r, 3r2
Product of first five terms = (3 /r2) x ( 3 /r ) x 3 x 3r x 3r2
= 243
54. The element of ith row and jth column of a determinant of third order is equal to 2(i+j). What is the value of the determinant?
(a) 0
(b) 2
(c) 4
(d) 6

= 8 [ 2(4 x6 – 5 x5) – 3(3×6 – 5 x4) + 4(3 x5 – 4 x4)]
= 8[ -2 +6 -4]
= 0
55. With the numbers 2, 4, 6, 8, all the possible determinants with these four elements are constructed. What is the sum of the values of all such determinants?
(a) 128
(b) 64
(c) 32
(d) 0
There are 24 (4 x3x2x1) 2X2 determinants possible with numbers 2, 4, 6 and 8
All values will either be +8 or -8
Sum = 8 +(-8) +8 +(-8) + …. +8 +(-8) = 0
56. What is the radius of the circle 4 x2 + 4y2 – 20x + 12y – 15 = 0?
(a) 14 units
(b) 10.5 units
(c) 7 units
(d) 3.5 units
4 x2 + 4y2 – 20x + 12y – 15 = 0
x2 + y2 – 5x + 3y – 15/4 = 0
x2 – 5x + y2 + 3y – 15/4 = 0
(x2 – 2. x. 5/2 + 25/4) + (y2 + 2. y .3/2 + 9/4) – 25/4 – 9/4 – 15/4 = 0
(x- 5/2)2 + (y + 3/2) 2 – 49/4 = 0
(x- 5/2)2 + (y + 3/2) 2 = (7/2)2
Radius = 7/2 = 3.5 units
57. A parallelogram has three consecutive vertices (-3,4), (0,-4) and (5,2). The fourth vertex is
(a) (2,10)
(b) (2,9)
(c) (3,9)
(d) (4,10)
Let ABCD be a parallelogram where A(-3,4), B(0,-4), C(5,2) and D(x,y).
AC and BD are two diagonals.
We know diagonals of parallelogram bisect each other.
The point of intersection of diagonals be (a,b).
Then a = (-3+5 )/2 = 1 , b = (4+2)/2 = 3
Also, a =(0+x)/2 =1
Therefore x = 2
b = (-4 + y)/2 = 3
Therefore y = 10
Fourth vertex is (2,10)
58. If the line y + px = 1 and y – qx =2 are perpendicular, then which of the following is correct?
(a) pq + 1 = 0
(b) p + q + 1 = 0
(c) pq – 1 = 0
(d) p – q + 1 = 0
Line y + px = 1 and y – qx =2 are perpendicular
y = – px + 1 and y = qx + 2
m1 = – p and m2 = q
Since two lines are perpendicular
Therefore m1 . m2 = -1
-p . q = -1
pq – 1 = 0
59. If A, B and C are in AP, then the straight line Ax + 2By + C = 0 will always pass through a fixed point. The fixed point is
(a) (0,0)
(b) (-1,1)
(c) (1,-2)
(d) (1,-1)
A, B and C are in AP
2B = A+C
A – 2B + C = 0 – (i)
The given straight line: Ax + 2By + C = 0 – (ii)
On comparing (i) and (ii), we get x = 1 ,y= -1
Fixed point: (1,-1)
60. If the image of the point (-4,2) by a line mirror is (4,-2), then what is the equation of the line mirror?
(a) y = x
(b) y = 2x
(c) 4y = x
(d) y = 4x
Slope = -1/2
Slope of mirror = 2
Midpoint of (-4,2) and (4,-2) is (0,0)
Since midpoint lies on y = mx+c
Therefore c = 0
Hence equation of the line mirror y =2x
61. Consider the following statements in the respect of the points (p,p-3),(q+3,q) and (6,3):
1. The points lie on a straight line.
2. The points always lie in the first quadrant only for any value of p and q.
Which of the above statements is/ are correct?
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2